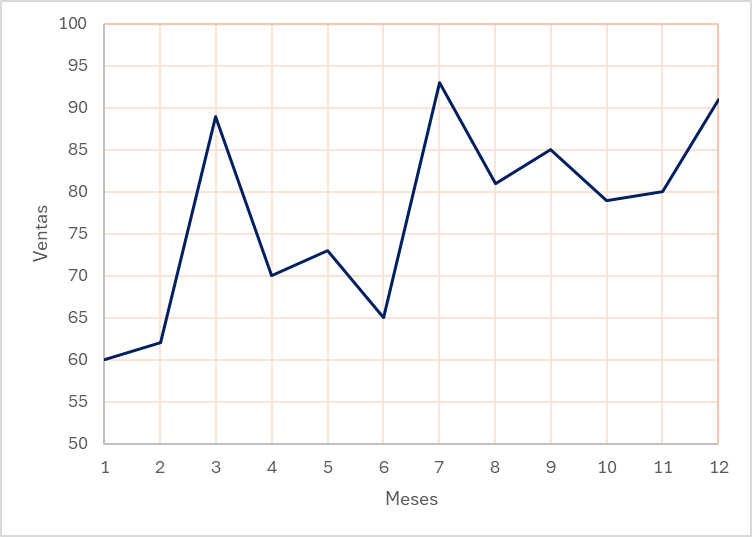
En artículos anteriores discutimos que dentro de los métodos cuantitativos para realizar pronósticos, las series de tiempo utilizan datos históricos para predecir futuros valores basándose en patrones identificables en el tiempo. La utilidad y valor de emplear estos métodos recae cuando el analista o encargado de realizar el pronóstico dispone de datos y que, a partir de su análisis se pueden identificar tendencias, ciclos y estacionalidades.

Para ejemplificar cada uno de los modelos, tómese en cuenta el siguiente problema propuesto:

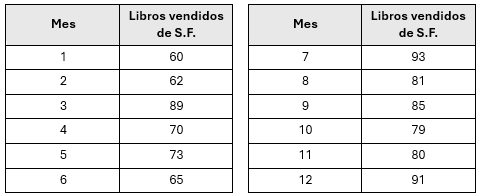
Una librería de la zona metropolitana de Torreón tiene registros de ventas de libros de ciencia ficción en edición de bolsillo, correspondiente a los 12 meses del año 2022. Los datos presentados se emplearán para el análisis de los modelos de pronósticos correspondientes.

Promedio móvil simple

El promedio móvil simple (SMA, por sus siglas en inglés) es un método que calcula el promedio de un conjunto fijo de valores pasados. Se utiliza para suavizar fluctuaciones a corto plazo y resaltar tendencias a largo plazo.

Su fórmula es la siguiente:

\[ \text{SMA}_t = \frac{1}{n} \sum_{i=0}^{n-1} A_{t-i} \]

donde \( A_t \) es el valor en el tiempo t y n es el número de períodos considerados en el promedio.

Ventajas:

• Fácil de calcular y comprender.

• Eficaz para datos sin tendencia o estacionalidad pronunciada.

Desventajas:

• No responde bien a cambios rápidos en la tendencia.

• Todos los valores en el período tienen el mismo peso, lo cual puede no ser adecuado en todos los contextos.

Retomando el ejemplo propuesto, para el cálculo de SMA con tres periodos móviles (N=3). Entonces para el primer intervalo del móvil es decir t +1 (=4):

\[ \text{SMA}_4 = \frac{60+62+89}{3} = 70.33 \approx{71} \]

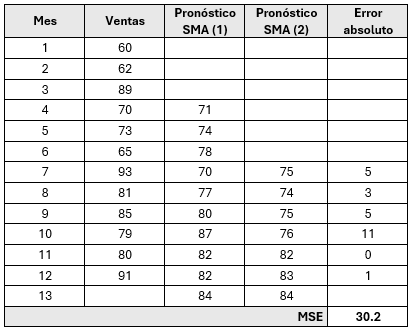
Entonces, la demanda pronosticada a tres periodos, junto con el error calculado en los meses que se tienen registro será:

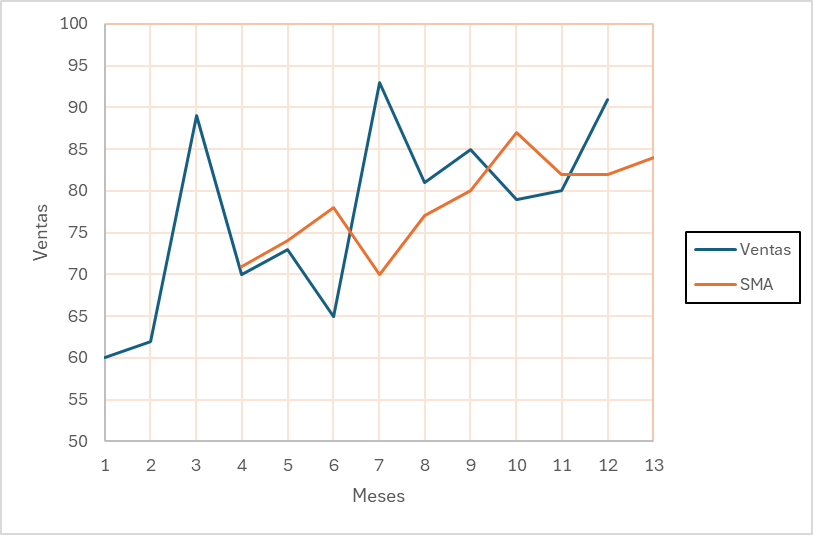
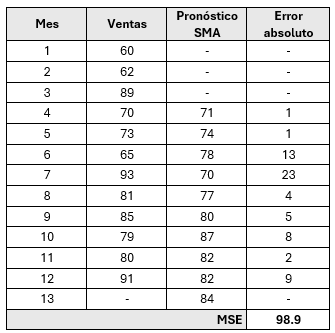
Promedio móvil ponderado

El promedio móvil ponderado (WMA, por sus siglas en inglés) asigna diferentes pesos a los valores en el período de cálculo, generalmente dando más peso a los valores más recientes.

Su fórmula es:

\[ \text{WMA}_t = \frac{\sum_{i=0}^{n-1} w_i A_{t-i}}{\sum_{i=0}^{n-1} w_i} \]

donde \( w_i \) son los pesos asignados a cada período \( i \).

Ventajas:

• Permite dar mayor importancia a los datos más recientes.

• Más adaptable a cambios recientes en la tendencia.

Desventajas:

• Requiere la determinación de los pesos, lo cual puede ser subjetivo.

• Más complejo de calcular que el promedio móvil simple.

Para el ejemplo, se asigna la ponderación con valor de 6 bajo los siguientes criterios

• Se asigna valor de 3 al periodo anterior al mes del primer intervalo móvil, es decir N-1.
• Se asigna valor de 2 al segundo periodo anterior al mes del primer intervalo móvil, es decir N-2.
• Se asigna valor de 1 al tercer periodo anterior al mes del primer intervalo móvil, es decir N-3.

Para el primer intervalo móvil, t=4

\[ \text{WMA}_4 = \frac{1(60)+2(62)+3(89)}{6} = 75.167 \approx{76} \]

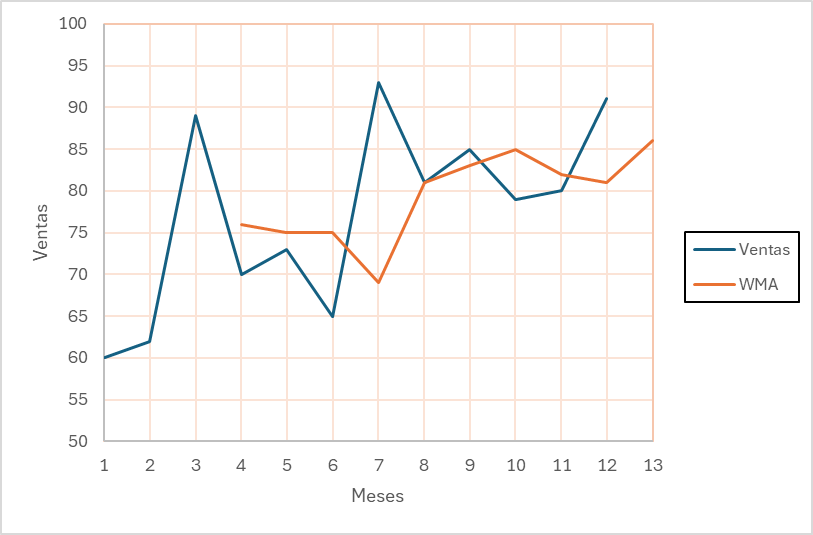
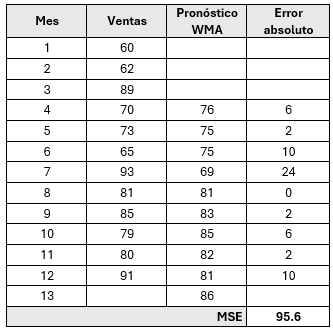
Promedio móvil doble

El promedio móvil doble es una técnica que aplica el promedio móvil simple dos veces para suavizar aún más los datos y detectar mejor las tendencias subyacentes.

Su fórmula es:

1. Calcular el primer promedio móvil simple (SMA).

2. Aplicar el promedio móvil simple nuevamente sobre los valores resultantes del primer SMA.

\[ \text{SMA}_t^{(1)} = \frac{1}{n} \sum_{i=0}^{n-1} A_{t-i} \]

\[ \text{SMA}_t^{(2)} = \frac{1}{n} \sum_{i=0}^{n-1} \text{SMA}_{t-i}^{(1)} \]

Ventajas:

• Mejora la detección de tendencias a largo plazo al reducir la variabilidad de los datos.

• Es útil para datos con ruido significativo.

Desventajas:

• Aumenta el retraso en la detección de cambios en la tendencia.

• Puede ser más complejo y menos intuitivo que otros métodos.

Retomando los valores obtenidos del SMA, calculamos el primer móvil doble, es decir t(6+1) = 7.

\[ \text{SMA}_7 = \frac{71+74+78}{3} = 74.33 \approx{75} \]

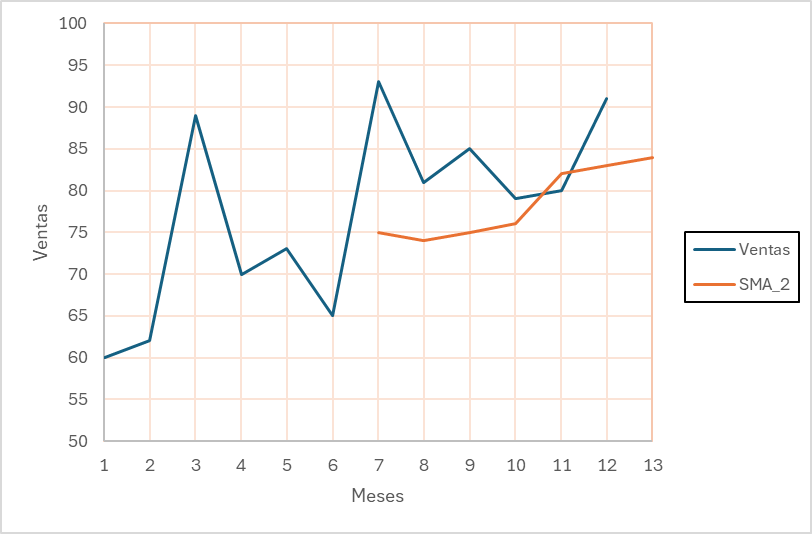
Suavizamiento exponencial

El suavizamiento exponencial es un método que aplica un peso decreciente exponencialmente a los datos históricos, dando más peso a los datos más recientes.

Su fórmula es:

\[ S_t = \alpha A_t + (1 - \alpha) S_{t-1} \]

donde \( \alpha \) es la constante de suavizamiento (0 < \( \alpha \) < 1).

Ventajas:

• Simple y eficaz para datos sin estacionalidad.

• Responde rápidamente a cambios recientes en los datos.

Desventajas:

• No maneja bien datos con tendencia o estacionalidad significativa.

• La elección de \( \alpha \) puede ser subjetiva.

Constante de atenuación:

La constante de suavizamiento \( \alpha \) determina el peso asignado a los datos más recientes. A continuación, se muestra una tabla que indica cómo \( \alpha \) afecta el peso relativo de los datos para diferentes períodos:

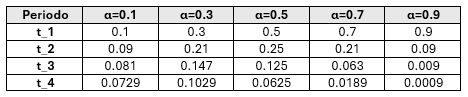
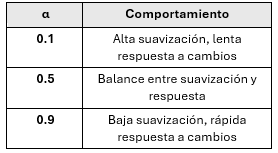
La constante de atenuación se elige típicamente entre 0 y 1. Su valor determina la velocidad con que los valores pasados pierden influencia.

Para el ejemplo, supóngase que el primer mes reportado fue de S = 64. Haciendo el cálculo para el primer periodo de suavizamiento t=2, con \(\alpha =0.1 \).

\[ S_2= \alpha (60) + (1 - \alpha) 64 = 0.1(60)+(0.9)(64)=63.6 \approx 64 \]

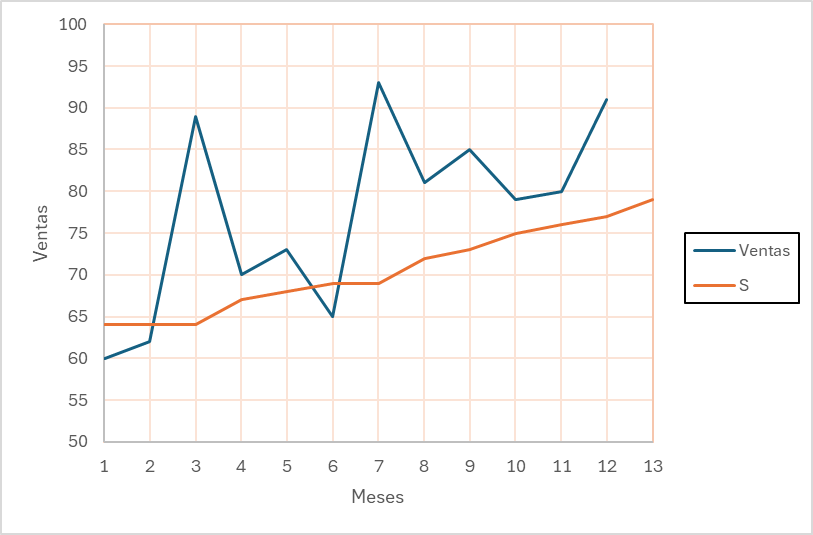
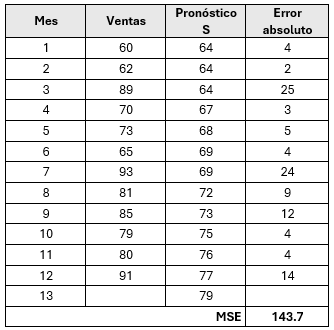
Si se hiciera con \( \alpha = 0.9 \) entonces:

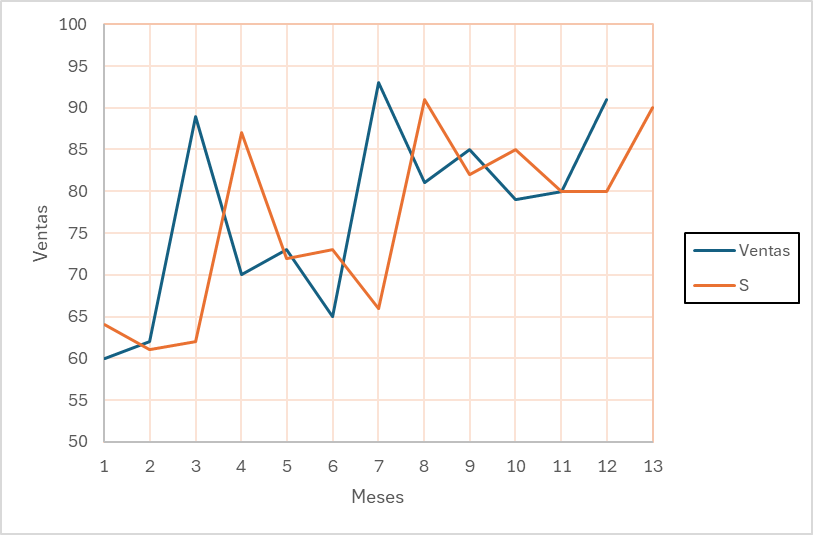
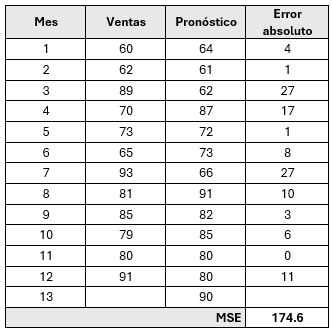
Suavizamiento exponencial doble

El suavizamiento exponencial doble es una extensión del suavizamiento exponencial simple que incluye una componente de tendencia para manejar datos con tendencia.

Su fórmula es:

\[ S_t = \alpha A_t + (1 - \alpha) (S_{t-1} + T_{t-1}) \]

\[ T_t = \beta (S_t - S_{t-1}) + (1 - \beta) T_{t-1} \]

donde \( \alpha \) es la constante de suavizamiento y \( \beta \) es la constante de tendencia.

Ventajas:

- Mejora la precisión en datos con tendencia.

- Ajusta tanto el nivel como la tendencia de la serie de tiempo.

Desventajas:

- Más complejo de implementar y ajustar que el suavizamiento exponencial simple.

- La elección de \( \alpha \) y \( \beta \) puede ser subjetiva y requiere ajuste fino.

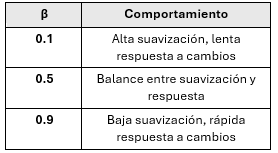
Constante de tendencia (\(\beta\)) y su comportamiento

La constante de tendencia también se elige entre 0 y 1. Su valor ajusta la sensibilidad del pronóstico a los cambios en la tendencia.

Para el ejemplo, utilizando una constante de suavizamiento de 0.3 y una constante de tendencia de 0.6, Si el pronóstico inicial es de 64 y la tendencia para el mismo periodo fue de 3, en el segundo periodo.

\[ S_2 = (0.3)(60) + (1 – 0.3) (64 + 3) = 64.9 \approx 65 \]

\[ T_2 = 0.6(65-64)+(1-0.6)(3)=1.8  \]

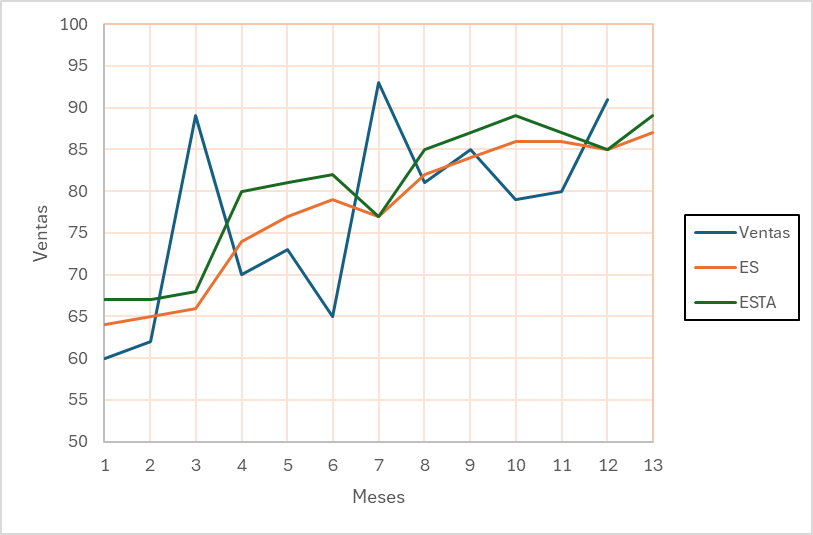
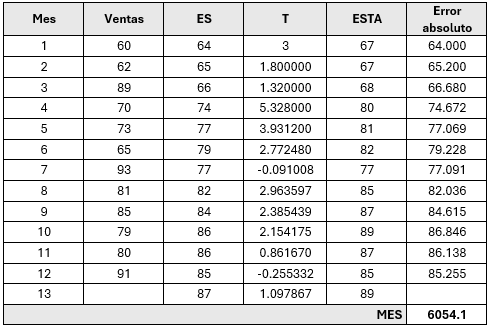
Se puede emplear el término de la suavización exponencial doble antes calculadas. Para ajustar y dar más fidelidad, se puede utilizar la suavización exponencial con ajuste a la tendencia (ESTA), que es la suma del pronóstico ( \(S_t\) ) con la tendencia en el periodo ( \(T_t \) )

\( \text{ESTA}_2 = S_t -T_t = 65+1.8=66.8 \approx 67 \)

En resumen, los métodos de pronóstico de series de tiempo son herramientas esenciales para analizar y prever datos futuros. La elección del método adecuado depende de la naturaleza de los datos y las necesidades específicas de precisión y complejidad.